Inductor Cores: Material and Shape Choices
This article provides a comparison of Magnetics powder and ferrite cores when used in inductors, including small and large DC inductors and large AC inductors. For additional assistance in determining a Magnetics core(s) to use in specific inductor designs, download our Inductor Design tool or contact Magnetics with your Custom Inductor Design request.
Introduction
An inductor is a current filtering device. By resisting change in current, the filter inductor essentially accumulates stored energy as an AC current crests each cycle, and releases that energy as it minimizes. Power inductors require the presence of an air gap within the core structure. The purpose of the gap is to store the energy, and to prevent the core from saturating under load. Another way to express the function of the air gap is to say that it reduces and controls the effective permeability of the magnetic structure. Since μ = B/H, the lower the value of μ, the greater the value of H (or current) that is supported at a level of B that is less than the maximum value of flux density (Bsat) inherent in the magnetic material. One envelope constraint is that Bsat is not widely variable. The physics of soft magnetic materials result in the case that commericially useful materials range from about 0.3T to 1.8T in Bsat.
The power inductor gap may be realized in one of two fashions, discrete or distributed. Distributed gap materials are powder cores. At a microscopic level, magnetic alloy powder grains are separated from one another by binder insulation or by high temperature insulation coating each grain. (This is not at the magnetic domain level; domains are vastly smaller than powder core grains.) Distributing the gap throughout the powder core structure serves two main purposes: (1) eliminating the disadvantages of a discrete gap structure, which are sharp saturation, fringing loss,and EMI, and (2) controlling eddy current losses so that higher Bsat alloys may be used at relatively high frequencies, despite comparatively low bulk resistivity in the alloy.
Discrete gaps are most commonly used in ferrite cores. The main performance advantage of ferrite is low AC core loss at high frequency, due to high material resistivity in the ceramic material, compared with metal alloys. Ferrites are at the low end of the available range for Bsat, and they shift down in Bsat significantly with increasing temperature. The discrete gap structure results in an inductor that reaches a sharp saturation point, requiring lots of headroom in the design. Discrete gaps also result in inductors that are vulnerable to eddy current losses in the coil due to fringing, and to generating EMI. Discrete gaps are also used in amorphous and nanocrystalline tape wound cut cores, which have improved AC loss performance compared with powder cores, but often at a cost disadvantage.
The inductor designer must meet the energy storage (inductance) requirement, as well as requirements for total loss, space, cost, EMI, fault-tolerance, temperature performance, and reliability. In the many cases powder cores have the clear advantage. Then the designer has a variety of options in choosing among the powder cores.
Core Material Properties
MPP (Molypermalloy Powder) cores are distributed air gap toroidal cores made from a nickel, iron, and molybdenum alloy powder. MPP exhibits second lowest core loss of the powder core materials (lowest being Kool Mµ Ultra), but it has the highest core cost due to processing costs and its 80% nickel content. MPP toroids are available from 3.5 mm to 125 mm in outside diameter.
High Flux cores are distributed air gap toroidal cores made from a nickel-iron alloy powder. Containing 50% nickel, and with processing costs comparable with MPP, High Flux pricing is typically 5%-25% less than MPP. High Flux exhibits higher core loss than MPP and Kool Mμ, but due to its higher Bsat, High Flux exhibits excellent performance in permeability vs. bias. In other words, higher Bsat translates into best inductance stability (least shift) under high DC bias or high AC peak current.
Kool Mμ® (or, “sendust”) cores are distributed air gap cores made from an iron, aluminum, silicon alloy powder. The Kool Mμ material is similar in DC bias performance with MPP. The absence of nickel in the formulation helps make Kool Mμ much more economical than the MPP. The main tradeoff is that Kool Mμ has higher AC losses than MPP. It is designed to be a practical alternative when iron powder is too lossy, typically because the frequency is moderate or high, but MPP is too expensive. In addition to toroids, Kool Mμ is available in a variety of geometries so that winding costs may be minimized.
Kool Mu® MAX powder cores, made of an alloy of iron, silicon, and aluminum, are an excellent choice for low core loss designs while still maintaining excellent DC bias performance. Priced between Kool Mµ and High Flux, Kool Mµ MAX cores prove to be cost efficient for a variety of applications. Currently available in toroids and two different blends for shapes - standard Kool Mµ MAX and Kool Mµ MAX "High Performance".
Kool Mµ® Ultra cores have the lowest core losses of any powder core material, with losses approaching that of ferrite cores while maintaining powder core advantages of soft saturation, stable high temperature performance, and no gap fringing losses. With DC Bias also superior to standard Kool Mµ and comparable to Kool Mµ Hf, Kool Mµ Ultra is a great choice for datacom and telecom applications. Currently available in toroids in 26, 40, and 60 permeabilities.
XFlux® cores are distributed air gap cores made from a silicon-iron alloy powder. The XFlux material exhibits slightly better DC bias performance than High Flux, and much better than MPP or Kool Mμ. The absence of nickel in the formulation helps make XFlux much more economical than the MPP or High Flux materials. The main tradeoff is that XFlux has higher AC losses than High Flux. It is designed to be an alternative when iron powder is too lossy or lacking DC Bias, or where the nickel alloys are too expensive or lack DC bias. In addition to toroids, XFlux is available in a variety of geometries so that winding costs may be minimized.
XFlux® Ultra powder cores offer the same high saturation found in standard silicon-iron XFlux while providing a 20% improvement in core loss. Currently available in toroids in 26 and 60 permeabilities.
| |
MPP |
High Flux |
Edge |
Kool Mµ |
Kool Mµ MAX |
Kool Mµ Ultra |
Kool Mµ Hf |
XFlux |
XFlux Ultra |
| Permeability |
14-550 |
14-160 |
14-125 |
14-125 |
14-90 |
26-60 |
26-125 |
19-125 |
19-60 |
| Saturation (Bsat) |
0.7 T |
1.5 T |
1.5 T |
1.0 T |
1.0 T |
1.0 T |
1.0 T |
1.6 T |
1.6 T |
| Max Temp (°C) |
200 |
200 |
200 |
200 |
200 |
200 |
200 |
200 |
200 |
| AC Core Loss |
Very Low |
Mod. |
Very Low |
Low |
Low |
Lowest |
Very Low |
High |
High |
| Core Shapes |
Toroid, Block |
Toroid, EQ, LP, EER, Block |
Toroid, E, U, Block, EQ, LP, EER |
Toroid, E, U, Block, EQ, LP, EER |
Toroid, E, U, Block, EQ, LP, EER |
Toroid |
Toroid, E, U Block |
Toroid, E, U, Block, EQ, LP, EER |
Toroid |
| DC Bias |
Mod. |
Better |
Best |
Mod. |
Good |
Good |
Good |
Better |
Better |
| Alloy Composition |
FeNiMo |
FeNi |
FeNi |
FeSiAl |
FeSiAl |
FeSiAl |
FeSiAl |
FeSi |
FeSi |
Table 1: Core Materials Comparison
Iron powder cores have higher core losses than MPP, High Flux, or Kool Mμ, but are generally less expensive. Iron powder is often the best choice for a power inductor when the highest efficiency and smallest size are not required, but cost is critical; or when the frequency is quite low; or when the amplitude of the AC ripple current is very low (resulting in very low AC flux, and thus reasonably low AC losses.) Most iron powder cores contain an organic binder for the grain-to-grain insulation that is susceptible to breakdown over time under high temperature operation, so the designer may need to take account of the thermal aging curves for the iron powder material being considered. Pressing densities (i.e. the compaction pressures) for iron powders are moderate, and consequently the materials are available in a variety of shapes including toroids, E-cores, pot cores, U-cores, and rods. For very large current inductors, unless the frequency is high, a large iron powder E, U or pot core may be the only practical alternative.
Gapped ferrite cores offer an alternative design option to powder cores. As Figure 1 illustrates, powder materials saturate gradually, and still maintain a useful, predictable inductance, even when the current load increases significantly. A gapped ferrite will maintain an inductance closer to the unbiased value until saturation occurs, where a sudden drop in inductance is seen. Some extra consideration must be taken when designing with ferrite at elevated temperatures. The flux capacity of any power ferrite is reduced significantly as temperatures rises, as shown in Figure 2, while the flux capacity of powder cores remains essentially constant over temperature.
The powder core soft saturation curve offers significant design advantages: (1) operating point well into the curve (80% to 50%) results in smaller size; (2) minimal shift with temperature; (3) minor sensitivity to variation in the curve, either due to temperature or material tolerances; (4) natural fault tolerance; (5) natural swinging inductance – high L at low load, controlled L at high load. Other advantages of the powder cores compared with ferrites are that they are not susceptible to fringing losses and gap EMI effects, and that they have higher inherent Bsat levels.
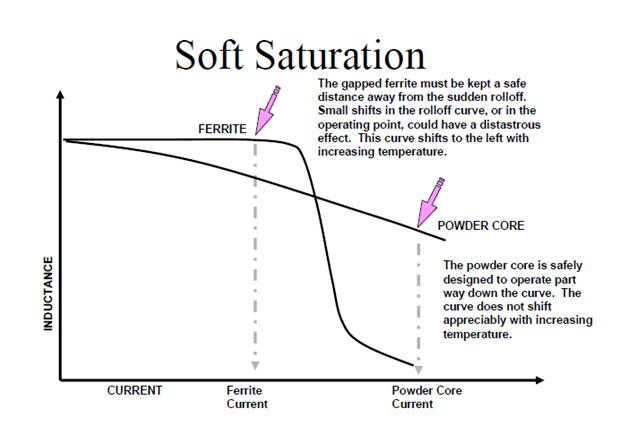
Figure 1 - DC Bias Curves for Ferrite and Kool Mu
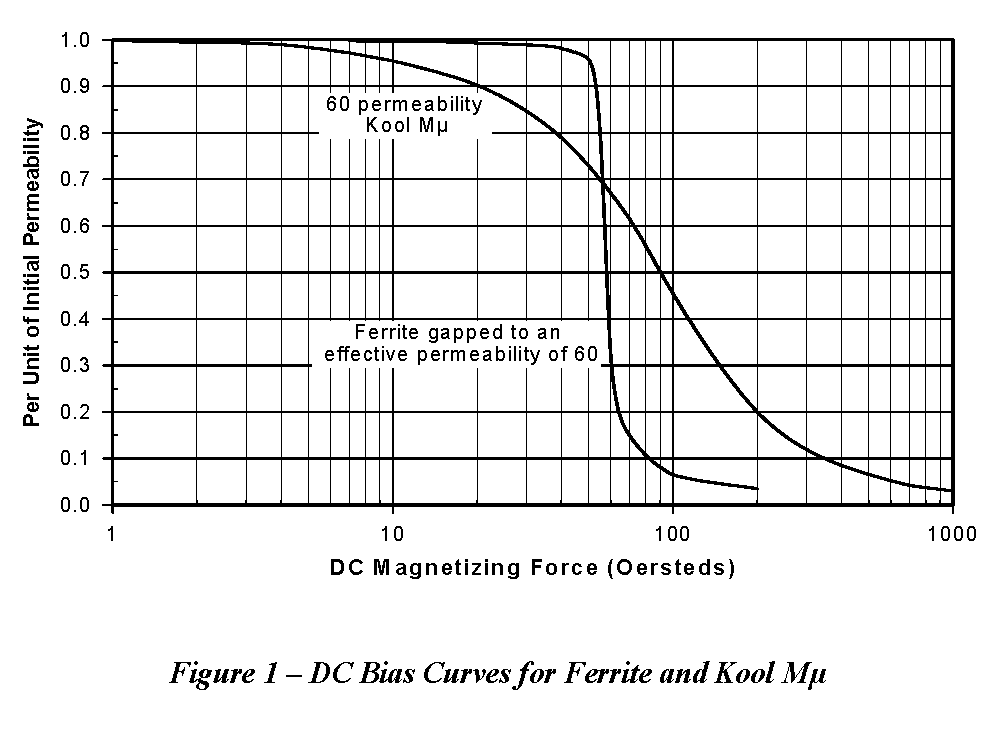
Figure 2 - Saturation Curve for Power Ferrite
.png.aspx)
Inductor Applications
Inductor application types include, among others:
1) A small DC inductor with small AC ripple current (window-limited design)
2) A large DC inductor (saturation-limited design)
3) An inductor with large AC current (core loss-limited design)
Each of these represents certain challenges in terms of design. A small DC inductor is typically limited more by the core’s available window area than its cross-section area. The core’s window must be large enough to accommodate the number of turns of wire required to reach the specified inductance. A large DC inductor is often limited by the core’s saturation point. The core must be large enough in size and low enough in permeability to avoid saturation (or shift in inductance below the minimum required level.) These factors increase the turns and length of copper required, causing wire loss to become an issue. An inductor with a large AC current is limited by core loss considerations. Since core loss is dependent on the AC flux swing, as opposed to the DC flux level, the core loss becomes the dominant factor in the design.
1. SMALL DC INDUCTOR DESIGN
As an example, the following requirements would represent a typical case:
DC current (Idc) = 500 mA maximum
Required Inductance (Lmin) = 100 uH
AC ripple current (Iac) = 50 mA peak-peak
Frequency (f) = 100 kHz
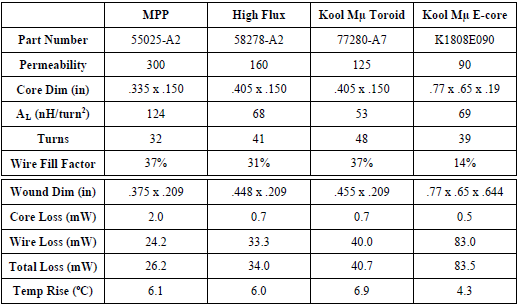
For the design of this inductor, Magnetics’ Inductor Design Tool, which uses Magnetics powder cores, is employed. This program uses a design algorithm intended to specify the smallest package size for the given input parameters (currents, inductance values, frequency, etc.) The program sizes the appropriate core based on the needed energy product, expressed as the full load inductance times the square of the peak (DC plus ripple) current flowing through the inductor. Higher inductance values and higher current levels imply a larger core size. The design tool was run with the above design inputs, and the core material was manually selected for each of the core types in Table 2 below. The turns, wire fill, wound dimensions, loss data, and temperature rise were taken from the tool outputs.
In each case, the design tool selected the highest permeability available in the material chosen. Because of the relatively small current, any reduction in the material permeability chosen would not result in an improvement in the inductance at peak load; in these cases, more is lost by the reducing the no-load inductance than is gained by improving the DC rolloff curve. Core losses and temperature rise are not a large factor in this type of inductor due to the core’s low operating AC flux density. For example, in the High Flux core, the magnetizing force H, is defined by Ampere’s Law:
- H (Oersteds) = .4(π)(N)(I)/Le, where
- N is number of turns
- I is current in amps
- Le is core’s magnetic path length in cm
The 58278-A2 has a path length of 2.18 cm, so that the DC magnetizing force is
- H = .4(π )(41)(.5)/(2.18) = 11.8 Oersteds
The percent of initial permeability or “roll off” value can be determined from Figure 3 - DC Bias Rolloff Curve for High Flux.
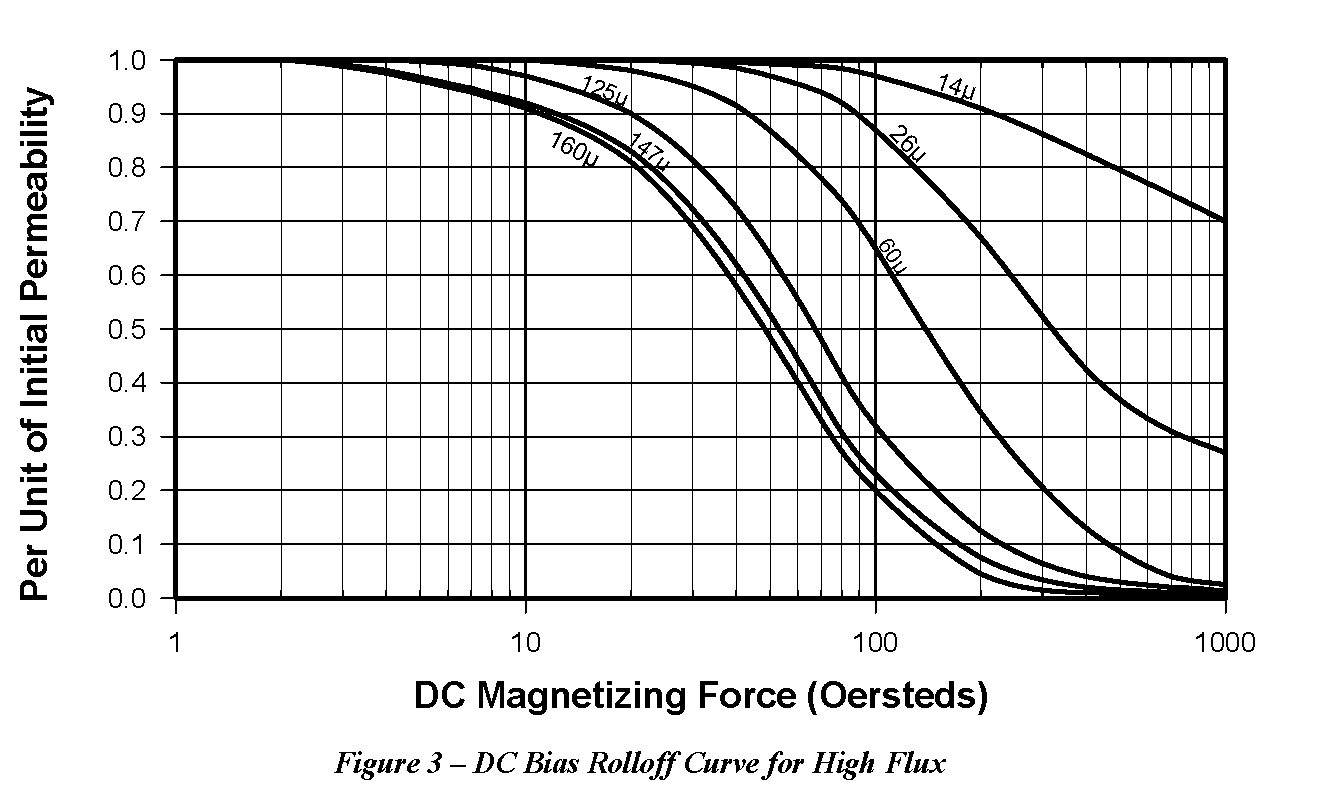
The graph for 160-permeability High Flux shows that the permeability under a DC bias of 11.8 Oersteds is approximately 90% of its initial value. This is a conservative operating point for this material, but the design is limited more by the core window area than the saturation of the core. The window fill factor for this inductor is 37%, which is approaching the typical limit for a toroid. Efforts to reduce core size in order to take advantage of the available flux capacity would result in unrealistic window fill factors of 50% or higher.
As the data illustrates, the MPP toroid yields the most compact and efficient design, due to the fact that this material is available in a higher permeability (300μ) as compared with the others. This translates into a higher inductance factor (AL) for a given core size, allowing a smaller core to be used. The trade off is that the DC bias rolls off sooner. The Kool Mμ toroid is attractive mainly by virtue of a significant cost advantage. The Kool Mμ E-core selected is the smallest currently available, and it is oversized for this particular set of requirements.
2. LARGE DC INDUCTOR DESIGN
As an example, typical requirements are:
- DC current (Idc) = 20 A maximum
- Required Inductance (Lmin) = 100 uH minimum
- AC ripple current (Iac) = 1 A peak-peak
- Frequency (f) = 100 kHz
- Max Temperature Rise = 40oC
Table 3 contains the pertinent information from the design output of the design tool for this case.
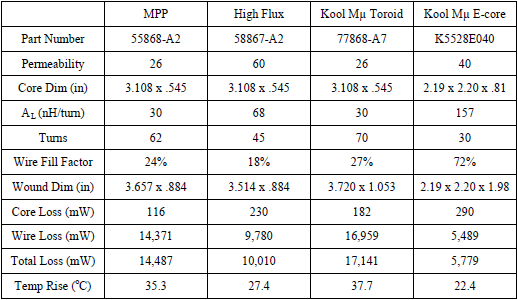
Table 3: Inductor Design Tool Output
For this inductor, the cores selected needed to be of lower permeability and large cross-section to avoid saturation under the high DC bias.
The 58867-A2 (C058867A2) has a magnetic path length of 20 cm. Again solving for magnetizing force H:
- H = .4(π)(45)(20)/(20) = 56.5 Oersteds
The graph for 60-permeability High Flux material in Figure 3 shows that the permeability is approximately 83% of its initial value under 56.5 Oersteds of DC magnetizing force, a safe operating point. Wire fill was not critical in this case, but temperature rise due to copper loss became the limiting factor. Further iterations of the design would be aimed at increasing the wire diameter, or multistranding wire for reduced current density, to reduce the copper loss, at a penalty of higher fill factors. From this data, we can see that the High Flux is the coolest running design of the toroids. The high saturation flux density of this material and better DC bias performance allows selection of a core with higher permeability and higher AL value, reducing the turns count and copper losses. Again, core losses are small due to the relatively small AC flux in the core.
The Kool Mμ E-core design is superior in terms of losses, due to the fact that the E-core’s cross section (and AL) is much larger than that of the toroids. This allows for fewer turns and dramatically lower copper losses. The E-core has a comparatively small window area, which results in a higher fill factor (72%), but this is achievable in a bobbin-wound construction. With the E-core, the option of using foil windings is available. The trade-off is that overall height of the E-core wound unit is approximately twice the other designs.
3. AC INDUCTOR DESIGN
Typical AC inductor requirements, for example, are:
- DC current (Idc) = 4 A nominal
- Required Inductance (Lmin) = 100 uH minimum
- AC ripple current (Iac) = 8 A peak-peak
- Frequency (f) = 100 kHz
- Max Temperature Rise = 35ºC
Unlike the previous two examples, small and large DC inductors, and the heat generated by core loss is significant enough in the AC inductor to become a primary design constraint. Temperature rise due to core loss, or efficiency targets, will limit the design choices. Table 4 contains the data for this example.
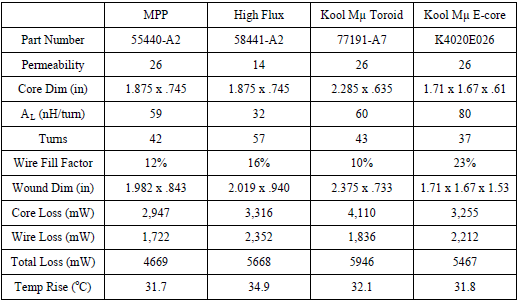
Table 4: Inductor Design Output
To determine core loss, the AC flux swing in the core in the core must be calculated. DC flux does not generate core loss. The first step is to calculate the magnetizing force H, by Ampere’s law using the AC current swing (8A pk-pk in this case). Considering the High Flux core, 58441-A2, the path length is 10.74 cm.
- H = .4(π)(57)(8)/(10.74) = 53.4 Oersteds
The change in flux density can be determined by applying this result to the databook normal magnetization curve (Figure 4.)
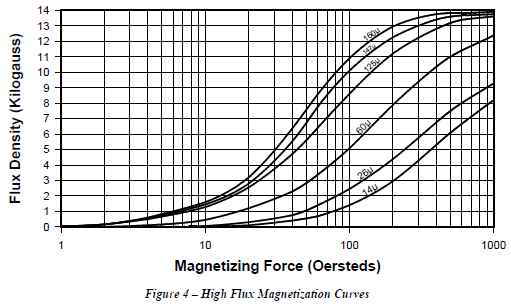
The magnetizing force excursion is from 0 oersteds to 53.4 oersteds. In the 14-permeability material this translates to a flux density excursion from 0 gauss to 600 gauss. I.e., the ΔB is 600G. Loss curves for soft magnetic materials presume bipolar operation (the core is driven into the 1st and 3rd quadrants of the BH loop.) Consequently, no matter whether the circuit is bipolar or unipolar, the flux density value that applies is always ½ΔB. In this case, the AC flux density is 300G. From Figure 5, for 300G at 100kHz, the loss density is about 150 mW/cc. From the databook, the volume of the 58441-A2 is found to be 21.3 cm3, so the total core loss is the product (150)(21.3) = 3195 mW. The design tool, using curve fit equations, calculated core losses of 3316 mW.
The temperature rise calculation is based on the following approximation.
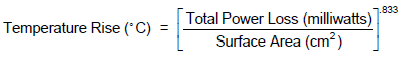
The total power loss for the High Flux inductor is 5668 mW from the tool. The 58438-A2 has a surface area of 69.3 cm2 bare, and 94.3 cm2 when fully wound (values are found in the databook.) The tool interpolates the surface area for a 17% wire fill factor, calculating a surface area of 79.3 cm2. So temperature rise is calculated from the above equation at approximately 35oC. Note that this is only a rough estimate as the thermal performance is a function not only of losses, but of mechanical configuration, assembly materials, and airflow.

In all, the superior loss characteristics of the MPP material allow for a smaller and more efficient inductor in this case. Total loss is 15% lower with the MPP than with the next best design. Since the High Flux material has higher losses, a lower permeability core must be chosen in order to keep core losses in check. This, however, results in more turns and more copper loss, and a slightly larger overall package. The reason that lower permeability tends to result in less AC flux density (and thus in lower core losses) is evident in the flatter slopes of the lower μ materials on the magnetization curves (Figure 4.) The Kool Mμ material results in a still larger overall size, but the total losses are comparable with the High Flux design. Again, there is the E-core option with Kool Mμ, which in this case has somewhat better losses, a smaller footprint, but larger overall height.
The Kool Mμ E-core is the lowest cost option of the four, while the MPP toroid’s advantage in size and efficiency is offset by being highest in cost. The High Flux core and MPP are the same size, and will be similar in price, since 14μ powders are more costly to produce and to press than 26μ powders.
Conclusion
For a given inductor, the material selection decision is informed by constraints of: space; efficiency; assembly; winding; total cost; inductance vs. load characteristic; temperature rise; and temperature rating. Among powder cores, MPP material is superior for core loss properties, and has highest available permeability. High Flux has an advantage when space and DC bias performance are critical constraints. Kool Mμ is consistently a lower cost option than MPP or High Flux, and is offered standard in both toroids and E-core geometries. Iron powder grades are lower still in cost than Kool Mμ, but with significant tradeoffs in performance.
Download PDFDownload Inductor Design ToolContact Magnetics